Der kleine Rote Traktor und das Sequenzkalkül

Sequenzkalkül

Also ähnlich wie das Sequenzkalkül der AL nur mehr.

Problem: freie Variablen die gabs in der AL ja nicht. Wir ersetzten alle freie Variablen durch "Konstanten" also aus $\psi(x_1, ..., x_n)$ wird zu $\psi(c_1, ... c_n)$

Also nun erweitern wir die Signatur $\sigma$ mit den Konstanten $\tau = \sigma \cup C$ und alle $\psi \in FO(\tau)$ sind zunüchst erstmal frei.

Eine Sequenz ist dann wieder $\Gamma \implies \Delta$ und ist gültig wenn alle Modelle von $\Gamma$ mindestens auch eine Formel aus $\Delta$ erfüllt.

Axiome sind:

Alle Formeln der Form $\Gamma, \psi \implies \Delta, \psi$ sind Axiome (logischerweise)

Die Schlussregeln sind:

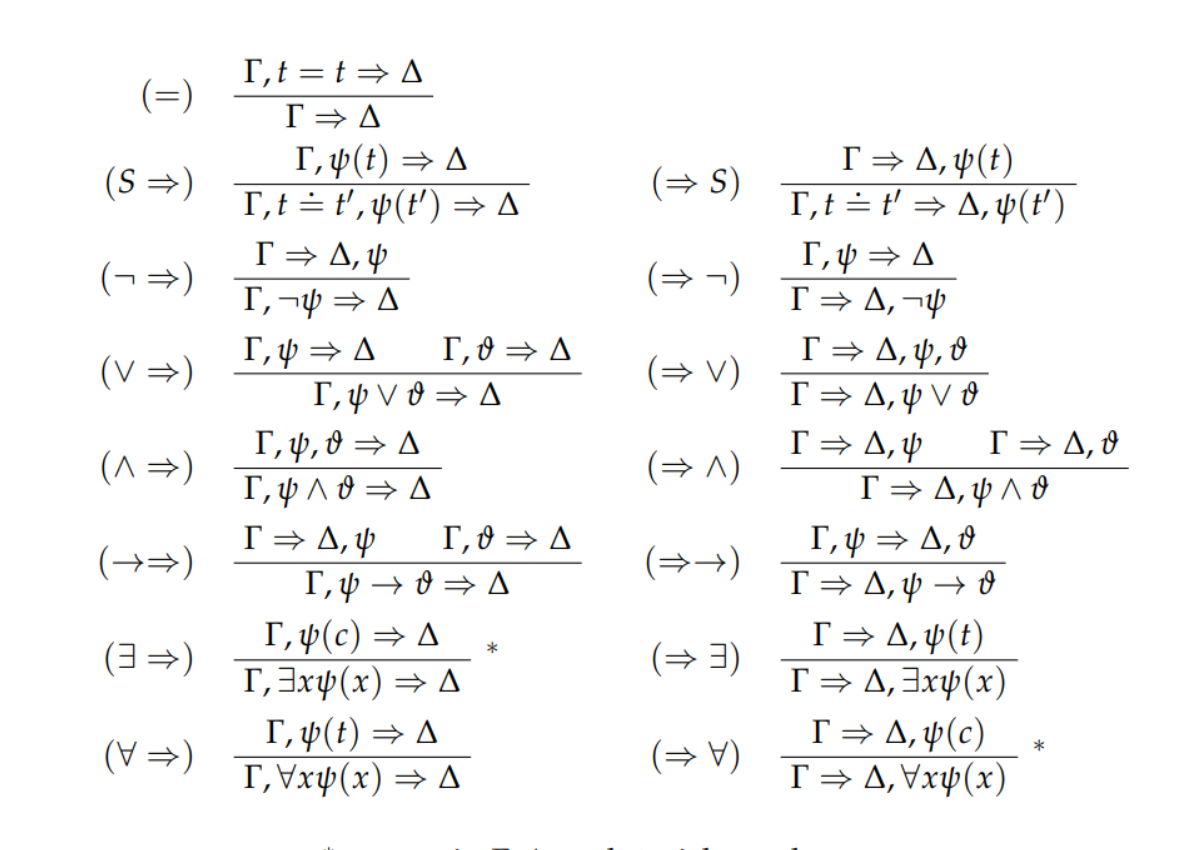
Ableitbarkeit

Eine Satz $\psi$ ist ableitbar aus einem Axiomssystem $\Phi$ ($\Phi \vdash \psi$), wenn eine endliche Teilmenge $\Gamma \subseteq \Phi$ existiert mit $\Gamma \implies \psi$

Eine Sequenz $\Gamma \implies \Delta$ ist ableitbar, wenn es eine ableitbare Sequenz gibt mit $\Gamma, \Gamma' \implies \Delta$ mit $\Gamma' \subseteq \Delta$

Eine Satzmenge $\Phi$ wo jeder Satz aus der Signatur ableitbar ist, heißt inkonsistent.

Jetzt wirds blöde: Vollständigkeitssatz

$\Phi \models \psi$ gdw. $\Phi \vdash \psi$.
$\Phi$ ist genau dann konsistent, wenn $\Phi$ erfüllbar ist.

Kanonische Modelle und Herbrand

Herbrand-Strukturen sind bissle irritierend. Sie besitzten genau die Elemente der Terme der Signatur. Vergesst also die Bedeutung hinter den Zeichen.

Genauer: Eine Herbrand-Struktur zu der Signatur $\tau$ (die min. ein Konstantensymbol erhält) ist eine $\tau$-Struktur $\mathfrak{H}$ Was ist im Universum drin: Alle Symbole (Grundterme) also für $\tau = \{+, 1\}$ z.B. $\{1, +\}$ Die Funktionen werden dann simple definiert $f^\mathfrak{H}(x_1, ..., x_n) = fx_1 ... x_n$ Also wir schreiben die sachen einfach hintereinander. Für $\tau = \{c,f\}$ also z.B. $c, fc, ffc, ...$

Die Relationen machen wir ähnlich: Für eine Herbrand-Struktur $\mathfrak{H}(\Sigma)$, wobei $\Sigma$ eine Menge von $\tau$-Sätzen ist.

$R^{\mathfrak{H}(\Sigma)} := \{ (t_1, ..., t_n) \mid Rt_1...t_n \in \Sigma\}$

Also wenn $\Sigma$ eine Kante $Rxy$ enthält fügen wir die auch bei der Herbrand-Struktur hinzu.

Gleichheit ist aber noch nicht gegeben, da zwei gleiche Terme wie 2 = +11 zwar in der Struktur stimmen, aber nicht in der Herbrand-Struktur: 2 ist halt eben nicht Syntaktisch gleich zu +11.

Kongruenzrelationen

Wir bilden also jetzt etwas was wir schon aus DS kennen. Eine Kongruenzrelation. Wir fassen alle Terme die in der Struktur die gleiche Bedeutung haben zusammen zu einem Ding (genauer zu einer Kongruenzklasse). Z.B. $2, 1+1, 1+1+1-1$ etc.

Die Kongruenzrelation $\sim$ ist also eine Äquivalenzrelation auf $A$.

Hierfür definieren wir: gilt $a_1 \sim b_1, ..., a_n \sim b_n$:

• $f^\mathfrak{A}(a_1, ..., a_n) \sim f^\mathfrak{A}(b_1, ..., b_n)$
• $(a_1, ..., a_n) \in R^\mathfrak{A}$ gdw. $(b_1, ..., b_n) \in R^\mathfrak{A}$

Und wir sagen $[a] := \{b \in A \mid a \sim b\}$ ist die Kongruenzklasse.

Aufpassen ab hier verwende ich wieder $[]$ als Kongruenzklasse und nichtmehr als Interpretations ausführung.

Faktorstrukturen

Was ist das jetzt schon wieder:

Wir haben jetzt alle Kongruenzklassen. Nun bündeln wir die Sachen zu einer Faktorstruktur $\mathfrak{A} / \sim$ zusammen

Also das Universum ist nun $\{[a] \mid a \in A\}$

Und wir definieren $f^{\mathfrak{A} / \sim}([a_1], ..., [a_n]) = [f^\mathfrak{A}(a_1, ..., a_n)]$ Genauso die Relation: $([a_1], ..., [a_n]) \in R^{\mathfrak{A} / \sim}$ gdw. ${(a_1, ..., a_n) \in R^\mathfrak{A}}$

Wir möchten jetzt Konzepte kombinieren

Wir haben Apple (Herbrand-Strukturen) und Pen (Faktorstrukturen) und möchten jetzt ApplePen machen.

Wir müssen aber trotzdem noch Sachen zu $\Sigma$ hinzufügen damit das Problem der Gleichheiten sich durch die Faktorstrukturen löst.

Hierfür

Eine Menge $\Sigma$ ist unter Substitution abgeschlossen, wenn für jede Formel $\psi(x)$ und jede Grundterme $t, t'$ gilt:

1. $\Sigma$ entählt $t=t$
   
2. Wenn $t=t'$ und $\psi(t) \in \Sigma$ dann auch $\psi(t') \in Sigma$

Wenn also jetzt $\Sigma$ (sonst erweitern wir $\Sigma$ halt) unter Substitution abgeschlossen ist, bilden wir eine Kongruenzrelation für die Herbrand-Struktur $\mathfrak{H}(\Sigma)$ bilden: Für bel. $t, t'$ Grundterme setzten wir:

$t \sim t'$ gdw. $t=t' \in \Sigma$

Dann nehmen wir die Faktorstruktur von der Herbrand-Struktur mit der Äquivalenzrelation und bekommen unser tolles:

$\mathfrak{A}(\Sigma) := \mathfrak{H}(\Sigma) / \sim$

Das heißt dann das kanonische Modell

Für jeden atomaren Satz $\psi \in FO(\tau)$ gilt: $\mathfrak{A}(\Sigma) \models \psi$ gdw. $\psi \in \Sigma$

Wofür das alles

Wofür brauch man das: gar nicht. Es sei denn man will den Volständigkeitssatz beweisen. Wollen wir aber nicht wurde ja schon. Hierfür braucht man aber auch noch Hintikka-Mengen die vllt wann anders mal mache. Für die Klausur sind aber Faktorstrukturen und Herbrand-Struktur durchaus wichtig.

Jetzt aber weiter zu den wichtigsten Sätzen der Vorlesung:

LS $\downarrow$: Jede erfüllbare abzählbare Satzmenge, hat ein abzählbares Modell

Kompaktheitssatz der Prädikatenlogik:

$\Phi$ ist erfüllbar gdw. jede endliche Teilmenge von $\Phi$ erfüllbar ist.
$\Phi \models \psi$ gdw. eine endliche Teilmenge $\Phi_0 \subseteq \Phi$ mit $\Phi_0 \models \psi$ existiert.

Und der zweite Löwenheim-Skolem:

LS $\uparrow$: Sei $\Phi \subseteq FO(\tau)$

1. $\Phi$ besitzt beliebig große Elemente (also für jedes $n \in \mathbb{N}$ ex. $\mathfrak{A}$ mit $|\mathfrak{A}| = n$). Dann hat $\Phi$ auch ein unendlich großes Modell.
   
2. Wenn $\Phi$ ein unendlich großes Modell besitzt. Dann gibt es zu jeder Menge $M$ ein Modell $\mathfrak{D} \models \Phi$ mit einem Universum das min. genauso Mächtig ist wie $M$.

Zudem:

Sei $\mathfrak{A}$ eine unendliche Struktur. Dann gibt es ein $\mathfrak{B}$ mit $\mathfrak{A} \equiv \mathfrak{B}$, aber $\mathfrak{A} \not\cong \mathfrak{B}$

Nichtstandard-Modelle

Ein Nichtstandard-Modell ist elementar äquivalent, aber nicht isomorph. Dank Skolem wissen wir: Es gibt ein abzählbares Nichtstandard-Modell der Arithmetik $\mathfrak{N} = (\mathbb{N}, +, \cdot, 0, 1)$

Außer dem PCP ist die Prädikatenlogik damit durch.