Reduktion deiner Note (semi-entscheidbarkeit & Aufzählbarkeit & Reduktionen)

Semi-entscheidbarkeit

Eine Sprache $L$ wir von einer TM $M$ erkannt, wenn jedes $M$ jedes Wort aus $L$ akzeptiert und kein Wort aus $\notin L$ akzeptiert (verwirft oder nicht hält)

Es ist klar, dass erkannt schwächer als entschieden ist denke ich.

Eine Sprache $L$ heißt semi-entscheidbar, wenn es eine TM $M$ gibt, die $L$ erkennt.

Das Halteproblem ist semi-entscheidbar, da wir einfach die Eingabemaschine simulieren können.

---

Semi-entscheidbarkeit und nicht semi-entscheidbarkeit ist nochmal was dolles. Merkt euch das:

• Falls $L$ semi-entscheidbar ist und $\overline{L}$ semi-entscheidbar ist, dann ist $L$ entscheidbar.
• Falls ihr also wisst, dass $L$ nicht entscheidbar ist, aber semi-entscheidbar, so ist $\overline{L}$ nicht semi-entscheidbar.
• Das Allgemeine Halteproblem $H_{all} = \{\langle M \rangle \mid M \text{ hält auf jeder Eingabe}\}$ ist nicht-semientscheidbar und sein Komplement ebenfalls nicht.

Aufzählbarkeit

Ein Aufzähler, ist eine Turingmaschine, die alle Elemente einer endlichen Menge $L$ aufzählt, heißt sie durckt nacheinander alle Elemente von $L$ auf ein Band.

Eine Sprache heißt rekursiv aufzählbar, wenn es einen Aufzähler für $L$ gibt.

$L$ rekursiv aufzählbar $\iff$ $L$ semi-entscheidbar.

(Polynomielle) Reduktion

Ich schätz wir müssen einen Reduktionsbeweis machen...

Seien $L_1$ und $L_2$ zwei Sprachen. Wir sagen, dass $L_1$ (polynomiell) reduzierbar auf $L_2$, wenn $L_1 \le_P L_2$. Merkt euch die Reihenfolge.

Das kleiner gleich Zeichen ist praktisch, da wenn z.B. $L_1$ unentscheidbar ist, dann muss $L_2$ auch unentscheidbar sein.

Also immer das größere ist mindestens gleichschwer.

Das gilt für alles mögliche:

• $L_1$ unentscheidbar $\implies$ $L_2$ unentscheidbar
• Aber auch andersherum: $L_2$ entscheidbar $\implies$ $L_1$ entscheidbar
• $L_1$ nicht semi-entscheidbar $\implies$ $L_2$ nicht semi-entscheidbar
• $L_1$ NP-schwer $\implies$ $L_2$ NP-schwer

Aber wie funktioniert jetzt eine Reduktion?

Wir brauchen eine Reduktionsabbildung $f: \Sigma^* \to \Sigma^*$, die für alle $x \in \Sigma^*: x \in L_1 \iff f(x) \in L_2$. Also kurz gesagt: $f$ muss alles akzeptierende von $L_1$ zu akzeptierende Wörter in $L_2$ mappen und alles verwerfende (nicht-haltende) von $L_1$ zu verwerfende (nicht-haltende) Wörter in $L_2$ mappen.

(Im Prinzip ist das einfach nur eine Art von Unterprogramm, nur in kurz und knapp).

Falls ihr die Korrektheit euerer Reduktionsabbildung zeigen müsst, müsst ihr folgendes zeigen:

• $w \in L_1$ \implies $f(w) \in L_2$
• $w \notin L_1$ \implies $f(w) \notin L_2$

Das (polynomielle) ist im Komplexitätsteil wichitg, da hier die Abbildung in polynomialzeit laufen muss.

PKP

Ich möchte hier noch einen kleinen Fokus aufs PKP legen, da ich im Gespür habe, man sollte das wissen. Das Postsche Korrespondenzproblem ist eine Menge von Doppel-Wörtern:

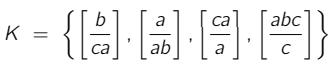
Das Ziel ist eine Folge von den Dominos (ihr könnt sie mehrmals und müsst nicht alle verwenden) zu finden, so dass sich oben und unten die gleiche Zeichenkette ergibt.

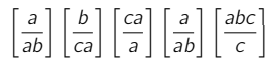
Überraschend aber wahr, eine Turingmaschine lässt sich mithilfe des PKP simulieren.