Unterprogrammtech-nick (Unterprogrammtechnik & Berechenbarkeitsbeweise)

Berechenbarkeit & Diagonalsprache

Der Grundstein unserer Beweiskette ist die Diagonalsprache. Sie zu verstehen hilft vielleicht und ich kann mir schon vorstellen, dass sie abgefragt werden kann.

$D = \{w \in {0,1}^* \mid w = w_i \text{ und } M_i \text{ akzeptiert w nicht } \} = \{ \langle M \rangle \mid M \text{ akzeptiert } \langle M \rangle \text{ nicht } \}$

Heißt eine TM M ist genau dann in $D$, wenn sie $\langle M \rangle$ (also ihre eigene Gödelnummer) nicht akzeptiert.

Warum ergibt dass dann ein Paradox?

Wiederspruchsbeweis, nehme an D ist entscheidbar.

Also gibt es eine TM M, die D entscheidet, heißt sie akzeptiert alles in D und verwirft alles $\notin D$. Nehmen wir nun $\langle M \rangle$ als Eingabe so gibt es zwei Möglichkeiten:

1. Fall $\langle M \rangle \in D \implies$ $M$ akzeptiert $\langle M \rangle$, da ja $M$ $D$ entscheidet (akzeptiert alles in $D$), $\implies \langle M \rangle \notin D$, durch die Definition von $D$.

2. Fall $\langle M \rangle \notin D \implies$ $M$ akzeptiert $\langle M \rangle$ nicht, da ja $M$ $D$ entscheidet (verwirft alles nicht in $D$), $\implies \langle M \rangle \in D$, durch die Definition von $D$.

Somit kann $D$ nicht entscheidbar sein.

Das Komplement von unentscheidbaren Problemen, ist selber unentscheidbar. Beispiel $\overline{D}$.

Unterprogrammtechnik

Mit der Unterprogrammtechnik lässt sich außerhalb vom Satz von Rice zeigen, dass eine Sprache unentscheidbar ist. Wie funktioniert es genau hier für das Beispiel des Halteproblems $H$:

Wir nehmen an das es eine TM $M_H$ gibt, die $H$ entscheidet.

Jetzt haben wir eine TM die was unmögliches kann, also müssen wir jetzt diese Funktion nutzen um zu zeigen, dass diese Funktion wieder ein anderes Problem (von dem wir schon die Unentscheidbarkeit wissen) lösen kann !ohne weitere Annahmen!.

Wir nutzen hierfür $\overline{D}$, bauen also eine TM $M_{\overline{D}}$, die $\overline{D}$ entscheidet und nutzen hierfür $M_H$.

Unsere TM $M_{\overline{D}}$ funktioniert folgendermaßen:

1. Teste ob die Eingabe $w$ eine Gödelnummer ist, wenn nicht, verwerfe, falls ja sei nun $M_w$ die TM mit $w = \langle M_w \rangle$.

2. Starte $M_H$ mit der Eingabe $ww$, also teste ob $M_w$ auf der Eingabe seiner eigenen Gödelnummer $w$ hält, oder nicht.

   -> Falls $M_H$ akzeptiert, heißt $M_w$ hält, simuliere mittels Universelle Turingmaschine $M_w$ auf der Eingabe $w$. Wir wissen dies hält an, also können wir es simulieren. -> Falls $M_H$ verwirft, verwerfe selber.

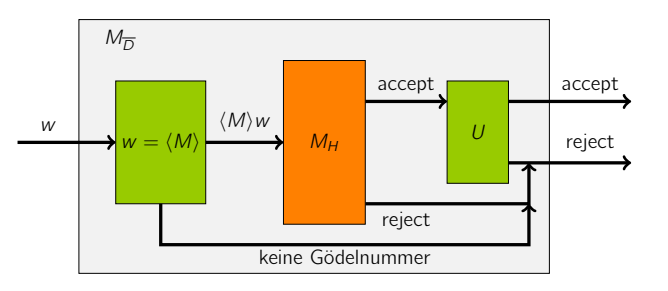
Also warum ist das hier jetzt ein Beweis.

Falls $w \in \overline{D}$ ist, dann akzeptiert $M_w$ $w$, heißt es hält an und akzeptiert dann beim simulieren.

Falls $w \notin \overline{D}$ ist, dann akzeptiert $M_w$ $w$ nicht, heißt es hält nicht an (verwirft) oder verwirft beim simulieren.

Wir können gleich nochmal ein anderes Problem per Unterprogrammtechnik beweisen, aber hier erstmal ein paar Tipps und Warnungen:

• Meistens muss man das Format einer Eingabe prüfen, es dann die Eingabe ggf. verändern (mit einer berechenbaren Funktion) und dann das Ergebnis in unsere Angenommene Eingabe pumpen.
• Mehr Tips muss ich mir noch überlegen :D