Physikalische Grundlagen

Vorwort

Hey ho! Hat dir meine Datkom zusammenfassung gefallen? Dann solls hier weiter gehen...

Zunächst mal Props an Dirk der powered den ganzen scheiß komplett alleine durch. Kennt ihr andere Fächer die von einer einzigen Person gehalten, korrigiert und beaufsichtigt wird? Außerdem ist Dirk ja sogar eigentlich nur im Studiencenter aktiv.

Nun hierzu. Ich werde alle Fachwörter (größtenteils markiert) auf Englisch schreiben klingt sonst komisch Rahmen im Protokoll zur Konvergenz der physikalischen Schicht.

Physikalische Grundlagen

Wie übertragen wir Daten ohne physikalische Verbindung? Elektromagentische Wellen.

Wir können verschiedene Größen variieren um Daten zu übertragen.

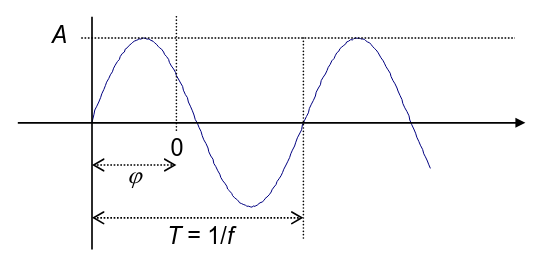
Zeichen	Name	Bedeutung	Einheit	Verwandheit
$A$	Amplitude	Stärk	k.P. ( $V/m$ 🤓)	-
$f$	Frequenz	Wiederholungen pro Sek.	$Hz$	-
$T$	Periodendauer	Zeit für eine Wiederholung	$s$	$1/f$
$\varphi$	Phase	Anfangsverschiebung	$rad$	-

Da wir ja über _Elektromagentische Strahlung also Licht reden ist die Geschwindigkeit fix bei $c \approx 3 \cdot 10^8 m/s$ und somit gibt es eine Wellenlänge $\lambda = c/f = c \cdot T$ . Ihr müsst das wissen, da oft die Wellenlänge angegeben wird.

Signals & Bandwidth

Wie genau wir nun bits mittels Wellencharakteristika $(A,f,\varphi)$ übertragen schauen wir sofort aber daraus entsteht ein signal (es enthält irgendeine Information).

Nun füren wir das zweite immens wichtige Fachwort ein bandwidth. Bandwidth beschreibt ein bestimmten Frequenzbereich (z.B. $20MHz$ ). Wir brauchen immer einen Bereich da 1) wir nicht immer Perfekt eine Frequenz treffen und 2) decomposition mittels Fouriertransformation Amplitudenänderung zu Frequenzbereichen führen.

Nyquist sagt uns Signalrate $S$ (Parameterwechsel pro Sekunde) $S_{max} [Hz] = 2 * B [Hz]$ und wir brauchen auch eine bestimmte Menge Parameter um $m$ bits zu dekodieren: $R_{max} [bit/s] = 2 * B [Hz] * \log_2(n) [bit]$

Amplitude Shift Keying (ASK): Wähl die Amplitude $A_1$ und jede andere Amplitude wird als low bit gewertet (oder eine bestimmte low amplitude). Doof nur das scheiße ist und einfach nicht möglich die Amplitude instant zu erhöhen.
Frequency Shift Keying (FSK): Ändere die Frequenz bei bit 1. Doof das wir noch mehr Bandwidth brauchen als bei ASK
Phase Shift Keying (PSK): Ich glaube selbsterklärend. Besser als ASK.
Advanced FSK / Minimum Shift Keying (MSK): Die gleiche Idee wie Manchester encoding. Jede Bit transition ist eine Frequenz und $f_2 = 2 \cdot f_1$ .
Binary PSK: $0$ Sinus. $1$ -Sinus.
quaternary PSK: kodier 2 bits in 4 Phases.
Quadrature Amplitude Modulation (QAM): Mach Amplitude und Phase zusammen. $16-QAM$ (4 bits werden zu einem signal)

Natürlich haben wir alle den gleichen Raum und hören deswegen zwangsweise bei anderen mit. Dieses noise interferiert leider mit unseren schönen Wellen und manchmal nuked es sie auch einfach komplett. $\text{SNR} = S / N$ ist die Signal-to-noise ratio in dezibel $\text{SNR}_{\text{db}} = 10 \cdot \log_10(S/N)$ .

Und Shannon sagt dann mal wieder $R_{max} [bit/s] = B [Hz] \cdot log_2 (1 + S/N) [bit]$ .

$min(\text{Shannon}, \text{Nyquist})$ gibt uns dann das maximale was wir (definitiv nicht) rausholenkönnen.

Antenne AC

Hier werden wir etwas skippen ist für uns glaube ich nicht sonderlich interessant. Wichtig ist die ideal antenna von einem Punkt ausgehent gleichverteilt in jede Richtung sendend. Das ist wie immer physikalisch unmöglich, echte Antennen sind anders:

Simple Dipoles: Stab in der Mitte um in herum ein Torus
Directed: Hier versuchen wir in eine x,z,y Richtung zu ballern.
anderes: gibt vieles.

Aber auch die sind nicht genau. Es gibt immer ein gewissen "leak" in alle Richtungen.

Wenn wir mehrere Antennen nebeneinander mit $\lambda / 2$ Abstand zueinander, aber mit dem passender Kabellänge zum transmitter installieren haben wir mittels Beamforming nun einen stärkere directed Antenne wo wir sogar teilweise die Richtung ohne Bewegung ändern können.

Die Signale werden grob quadratisch zum Abstand vom Sender schwächer (ist ja logisch das Signal breitet sich ja im Raum aus). Genauer $P_{\text{receive}} = P_{\text{transmit}} \cdot (\frac{\lambda}{4 \pi d})^2 \cdot G_{\text{receive}} \cdot G_{\text{transmit}}$ . $d$ ist Distanz, $P$ Power. $G$ bedeuted Gain also Stärke im Vergleich zu der Idealen Antenne (muss ja Richtungsbezogen sein). Diese Rechnung ist aber noch viel zu optimistisch.

Wir haben nämlich ein Grundlegendes Problemchen multipath propagation. Was geil im MPTCP und Quic ist, ist hier kacke da das Signal auf direktem Weg schneller ist als erst am Porsche 911er abzuprallen und dann zu mir. Dieser Zeitverlust ist aber eine Phasenverschiebung und kann damit einfach wenns doof läuft das nächste Signal meiner direkten Übertragung ausradieren.

Oder es kann gut laufen und es wird besser oder ich bekomme einfach nur mehrere Kopien meines Signals, aber wir müssen alles erwarten :/.

Lösungen:

Erneut mehrere Antennen verwenden, die Interferenzen können ja nicht genau gleich sein, da die Wellen aus unterschiedlichen Richungen kommen.

Multiplexing

Multiplexing wir senden mit verschieden Wellenparameter. Sodass nicht jeder mit dem gleichen Wellenparameter sendet.

Frequency: Wir teilen das gesamte Spektrum in verschiedene channel ein. Statisch in der Spezifikationen beschriben

1.5. Orthogonal Frequency Division Multiplexing (OFDM): teilt den Frequenzbereich auch ein aber in mehrere Überlappende Bereiche hier können wir dann die anderen multiplexing Sachen auch noch anwenden und bekommen ein halbwegs gute Verbindung aber auch nicht unnötigen Ineffizenzen.
Time: Nur einer sendet Gleichzeitig (Einteilung in Timeslots). Frage: Wann senden wir?

is it my turn?

Um zu koordinieren muss jeder eine genaue Uhrzeit haben. Zusätzlich am besten guard times zwischen den Sendern für weniger Interferenzen und ungenaue Uhren.
Code: wir senden alle gleichzeitig unterschiedliches $\text{daten} \oplus \text{einzigartigem code}$ . Müssen dann aber herausfinden was eine Sender im gebrabel gesendet hat hierfür brauch er den Code vom Sender $(\text{empfangen} \oplus \text{code} = \text{daten})$ .
Space Multiplexing: Wir verwenden alles aber nur hier. Nächste Cell verwenden wir z.B. eine anderen Frequenzbereich.

Codes

Yippi es darf nie fehlen schöne gut coding algos. Das wichtigste ist Forward Error Correction auf allem. Bit Error Rate ist in jedem Fall verdammt kacke im Vergleich zu Kabeln. Wir brauchen gute error correcting codes. Hamming mit 1-bit fehlern reicht uns definitiv nicht!. Ich fokusier mich auf 2.

Block Codes. Aufteilung der Daten in blocks.
Convolutional $(n,k,K)$ -Codes. $n$ -bit output $k$ -bit input convoluded (📟 verrechnet) mit den vorherigen $K-1$ outputs.
```
graph LR
		A[Input bits] --> B[un]
		B --> C[un-1]
		C --> D[un-2]

		%% XOR-Kreise
		XOR1((⊕)) -->|+ un| V1[v<sub>n1</sub> = un ⊕ un-1 ⊕ un-2]
		XOR2((⊕)) -->|+ un| V2[v<sub>n2</sub> = un ⊕ un-2]

		%% Verbindungen zu XOR
		B --> XOR1
		C --> XOR1
		D --> XOR1

		B --> XOR2
		D --> XOR2
```
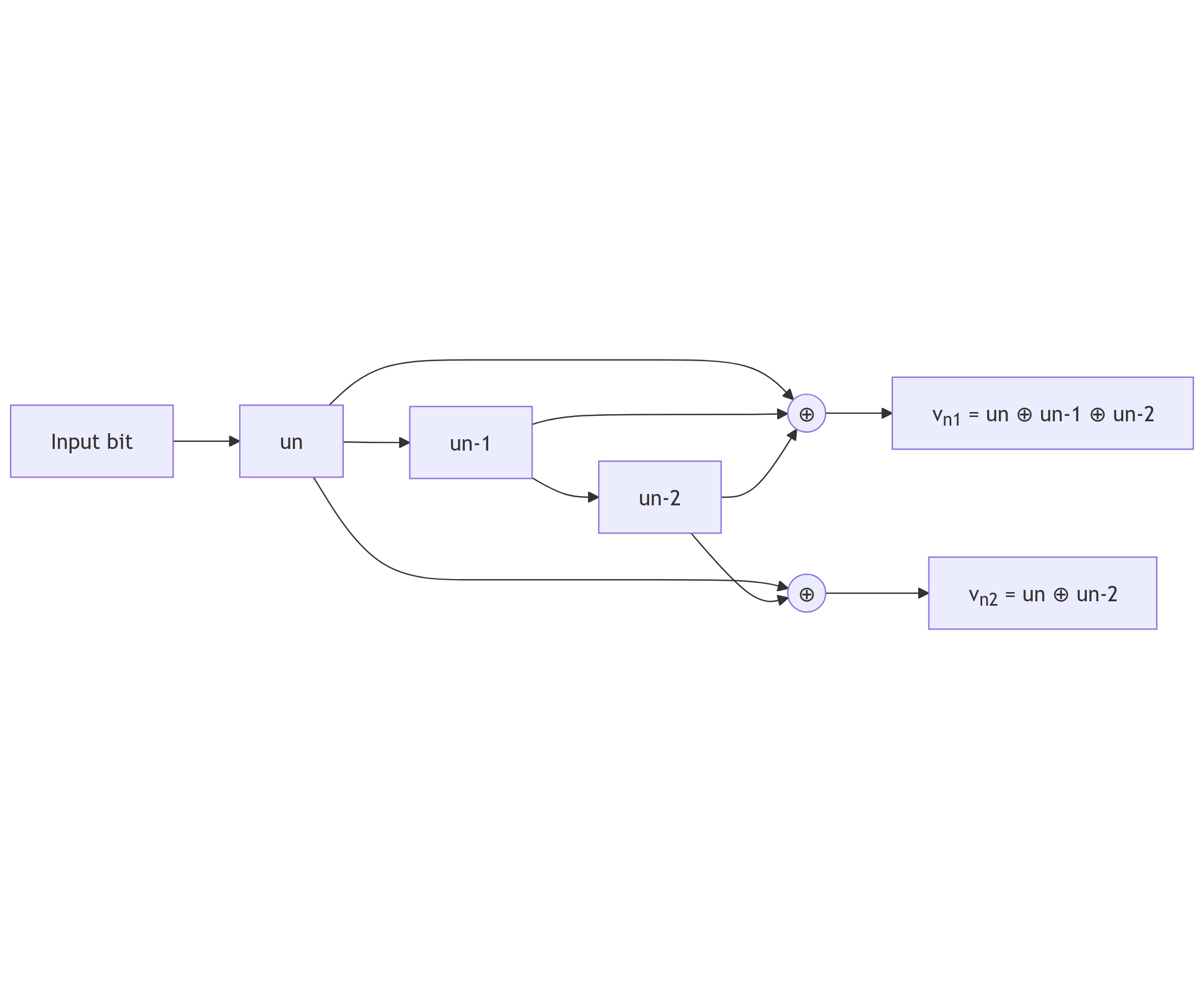
Bei $(2,1,3)$ sind die output $v_{n1} = u_{n-2} \oplus u_{n-1} \oplus u_n$ und $v_{n2} = u_{n-2} \oplus u_n$ . Encodieren ist extremst schnell und unaufwendig mittels Shiftregister. Decodieren ist dafür ziemlich pain. Hierfür erstmal das Zustandsdiagram

State Diagram

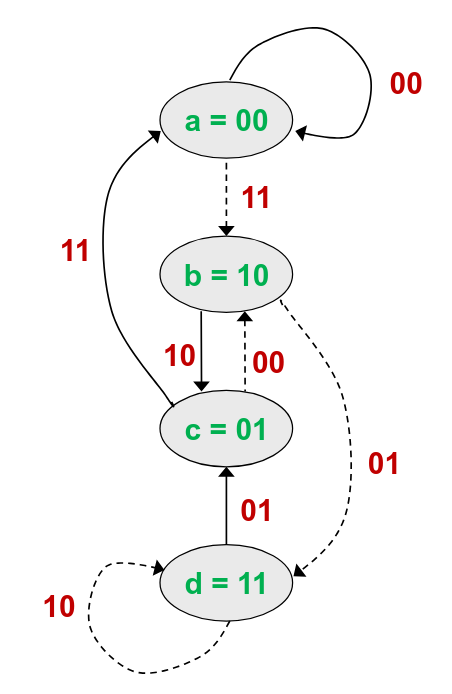
So ein Zustandsdiagram führen wir dann Zeitlich nacheinander auf zu einem trellis Diagramm.

Trellis Diagram

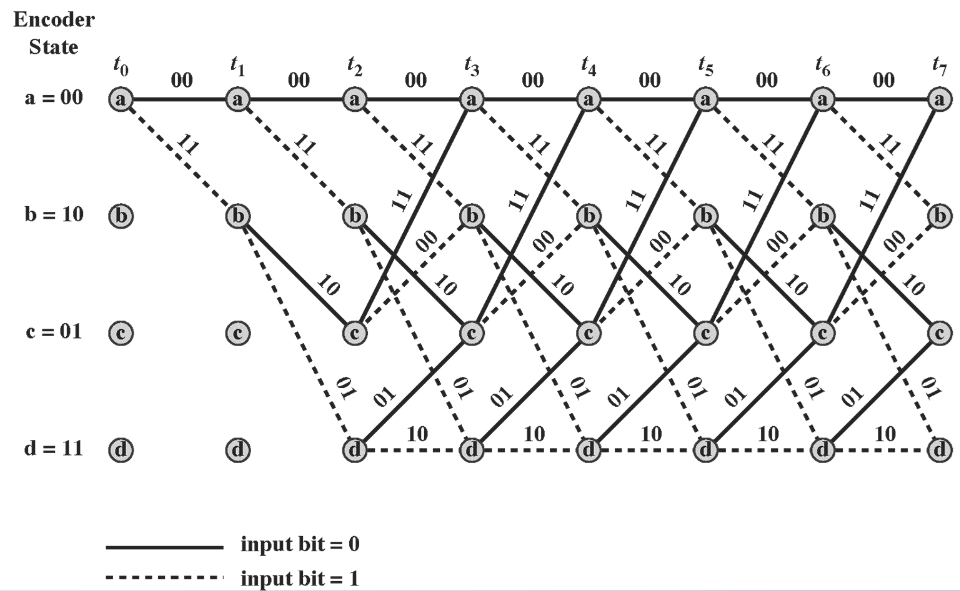
Oft nehmen wir an das wir bei 0 anfangen und auch wieder bei 0 aufhöhren müssen. Nun zum dekodieren können wir verschieden taktiken fahren. z.B. nehmen wir immer das nächst passende. Oder wir nutzen den Viterbi algo: Vergleiche die erhaltene mit allen !validen! Pfaden (heißt die müssen bei 0 enden). Nimm dann die Hammingdistanz und wähl den besten. Scheiße aufwändig auch in Klausur also lass mal lieber sein.
Turbo codes sind einfach nur ne Verbesserung von den gleichen Ideen die convolutional codes haben.

Nevertheless, CRC needed to check corrected frames on correctness

Back to Overview | Nächstes: MAC Nuggets