Pippi Langstrumpf löst die Re(v|s)olution auf (Kalküle)

Resolutionskalkül

Auch das Resolutionskalkül arbeitet mit KNF.

Eine Klausel ist hier einfach eine Menge von Literalen, die oft als Mengen dargestellt. Es entfällt somit Anzahl und Reihenfolge: $(X_1 \lor \lnot X_2) \land X_3$ wird zu $\{X_1, \lnot X_2\}, \{X_3\}$.

$\Box$ bezeichnet die leere Klausel.

• Die leere Klauselmenge ist erfüllbar

Nun bilden wir Resolventen $Res(K) := K \cup \{C \mid C$ Resolvente zweier Klauseln aus K $\}$

Eine Resolvente ist $\{X_1, X_2\}, \{\lnot X_1, \lnot X_2\}$ folgt z.B. $\{X_1, \lnot X_1\}$ wir gucken also immer nach $X$ ist einer und $\lnot X$ in einer anderen Klausel.

Dann gilt $Res^0(K) = K, \quad Res^{n+1} = Res(Res^n(K)) \quad Res^*(K) = \bigcup Res^n(K)$

Wir löschen also keine Sachen, sondern fügen nur die Resolventen hinzu.

Eine Klauselmenge ist genau dann nicht erfüllbar, wenn $\Box \in Res^*(K)$

Damit ist das Klakül:

• Korrekt: Es sind keine falschen Sachen ableitbar
• Vollständig: Alle wahren Aussagen können abgeleitet werden.

Sequenzkalkül

Eine Sequenz $\Gamma \implies \Delta$ gilt wenn jedes Modell von $\Gamma$ eine oder mehrere der Formeln aus $\Delta$ erfüllt.

Also $\bigwedge \Gamma \models \bigvee \Delta$

• $\Gamma \implies \emptyset$ gültig, genau wenn $\Gamma$ unerfüllbar
• $\emptyset \implies \Delta$ gültig, wenn $\Delta$ Tautologie ist.

Und nun Schlussregeln (kommen nicht zum Schluss das sind Axiome):

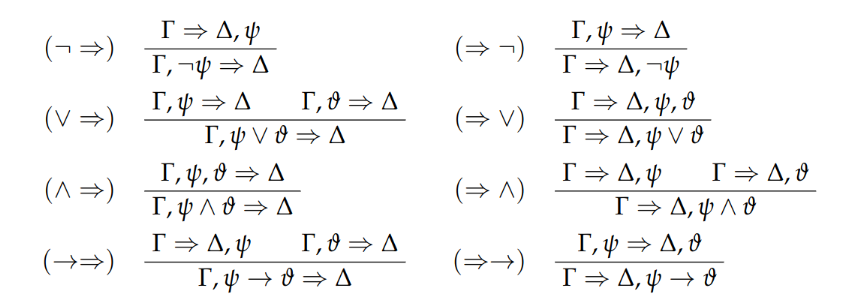
Und dann kan man das wie folgt anwenden (wohlgemerkt es ist bottom up also von unten nach oben):

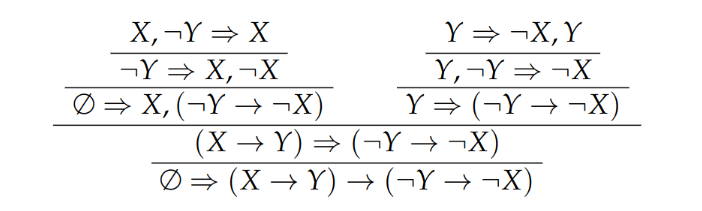
Die letzten beiden sind nach kurzem überlegen trivialerweise Axiome.

Doch wenn bei einer Ableitung etwa $X \implies Y$ und $Y \implies X$ kommt, bildet das Sequenzkalkül eine Falsifizierende Interpretation (nur bei AL)

Pippi Langstrumpf gefällt vor allem:

• Seq. ist korrekt und vollständig

Aufgaben für Pippi Langstrumpf